約60年にわたり未解決だった数学の難問「ソファを動かす問題」を、韓国の数学者、ペク・ジノン博士(31)=高等科学院・許埈珥数学難題研究所=が解決し、注目を集めている。
米国の科学専門誌「サイエンティフィック・アメリカン」は、2025年の「10大数学イノベーション」の一つとして、ペク博士による研究を選定した。この研究は、長年「最適性が証明されていなかった」ソファを動かす問題に、初めて理論的な決着をつけた点が高く評価された。
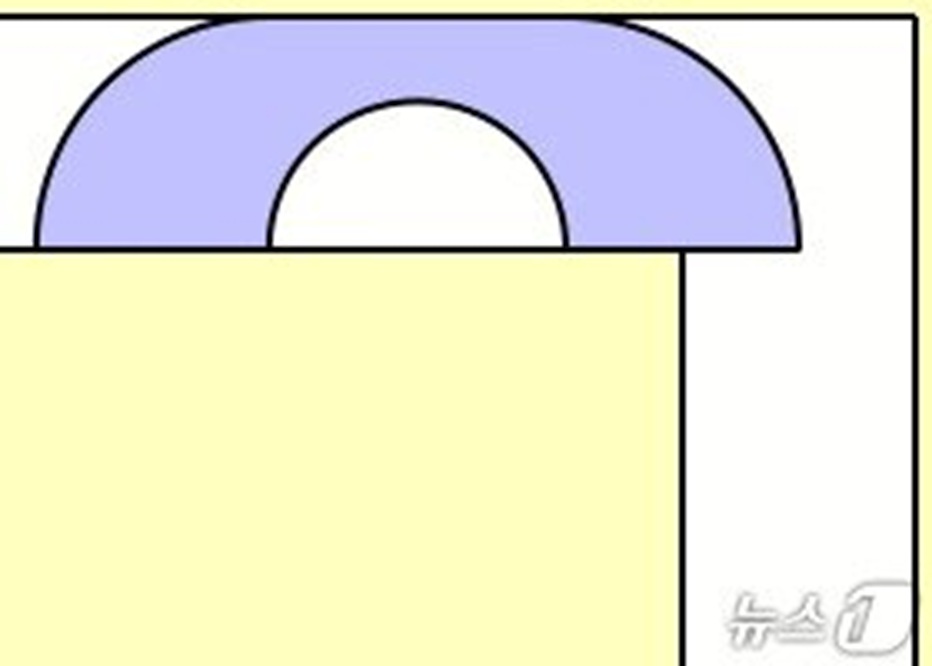
ソファを動かす問題とは、幅が1の直角に曲がった狭い廊下を通過できる図形のうち、最大の面積を持つ形は何かを問う問題。1966年にカナダの数学者レオ・モーザーが提起して以降、直感的に理解できる難問として知られ、米国の数学教科書にも掲載されてきた。
これまで多くの数学者がさまざまな図形を提示してきたが、最適解であることを厳密に証明することはできなかった。1968年には英国の数学者ジョン・ハマースリーが面積約2.2074の図形を示し、1992年には米国の数学者ジョセフ・ガーバーが18本の曲線から成る面積2.2195の図形、いわゆる「ガーバーのソファ」を発表した。しかし、この図形が最大であることは長らく未証明のままだった。
ペク博士は約7年にわたる研究の末、2024年末に全119ページの論文をまとめ、ガーバーのソファよりも広い面積を持つ図形は存在し得ないことを証明した。従来の研究が主にコンピューター計算で上限を絞り込む方法に依存していたのに対し、ペク博士は論理的推論を中心に最適性を示した点が大きな特徴だ。
この研究成果は、数学界で最高権威の一つとされる学術誌「アナール・オブ・マセマティクス」に投稿され、現在は査読・検証を待っている。
(c)news1

